学习自

有不足的望大佬们批评指正orz，此文仅作为学习笔记

神经网络的结构

神经网络有许多变体，例如**卷积神经网络（CNN）、递归神经网络（RNN）、转换器（transformers）**等等。

我们用来识别数字的简单网络，只是连接在一起的几层神经元

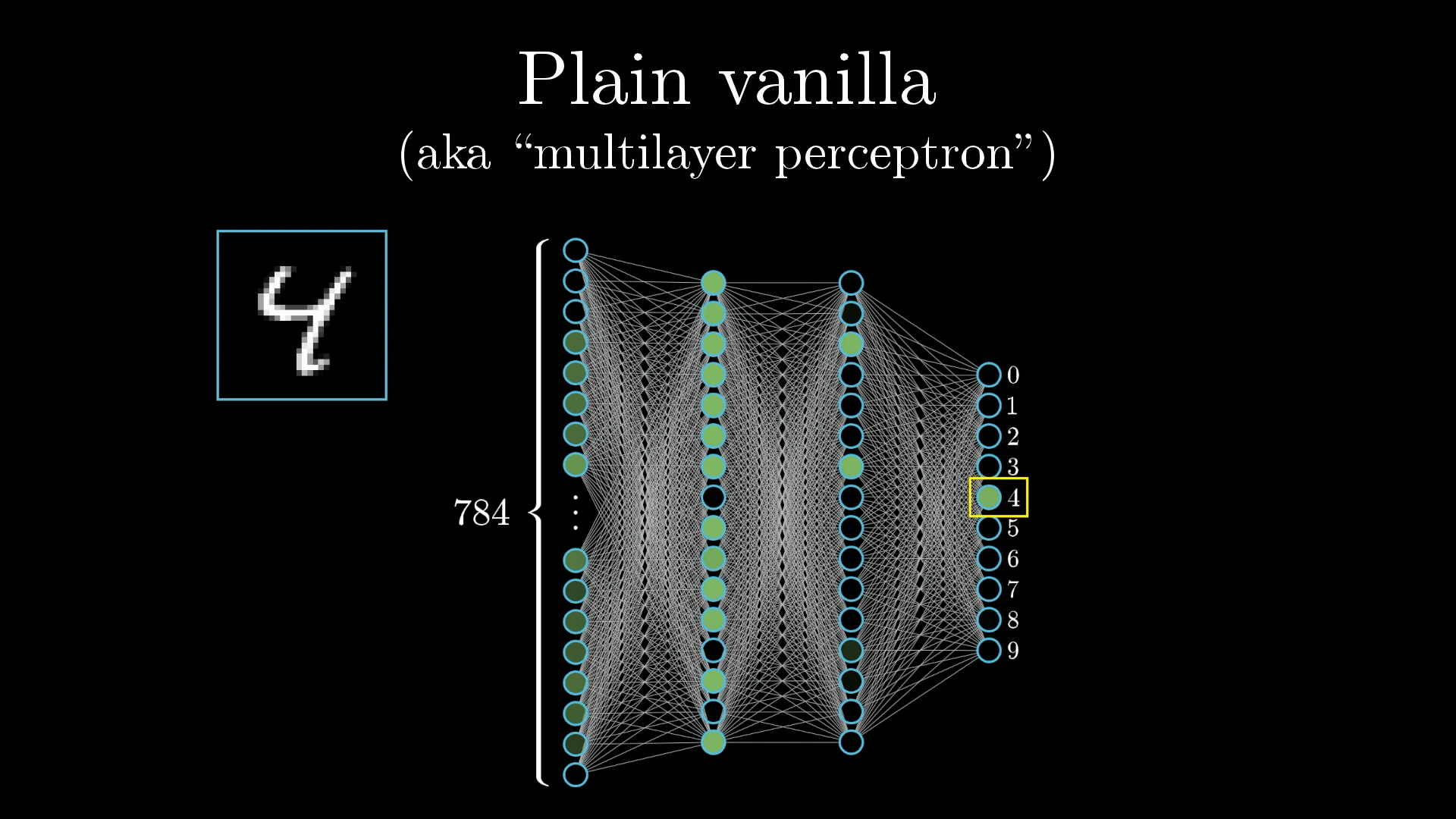
神经元(Neurons)

实际上，神经网络只是一堆连接在一起的神经元

在先前的识别数字的网络中，我们可以将神经元看作一个”包含数字的东西“，介于0.0与1.0之间

神经元内部的这个数字被称为该对应神经元的”activation(激活)”，可以构想这样一幅场景：当神经元的activation很高时，对应的神经元就会被**”点亮”**

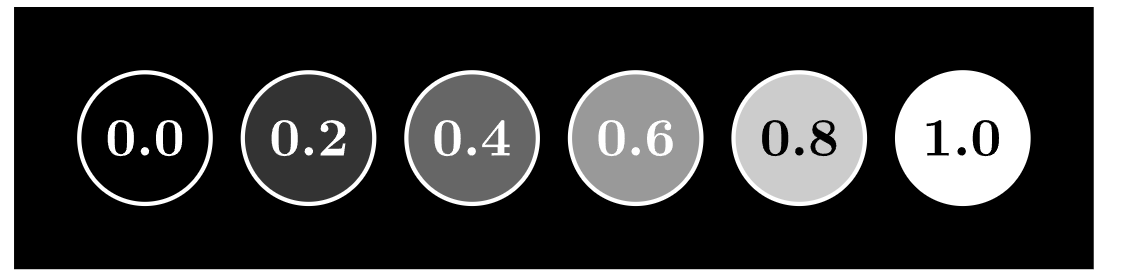
每个神经元的activation都在 0.0 到 1.0 之间，有点类似于大脑中的神经元如何活跃或不活跃。

通过我们神经网络的所有信息都存储在这些神经元中

我们需要使用这些介于0.0与1.0之间的神经元数值来表示网络的输入和输出（描述图像和数字预测）

原始图像中每个像素值介于0.0（完全黑色）和1.0（完全白色）之间

为了在网络中表示这一点，我们创建一个由784个神经元组成的层，其中每个神经元对应一个特定的像素

当我们向网络提供图像时，每个输入神经元的激活都被设置为对应像素的亮度

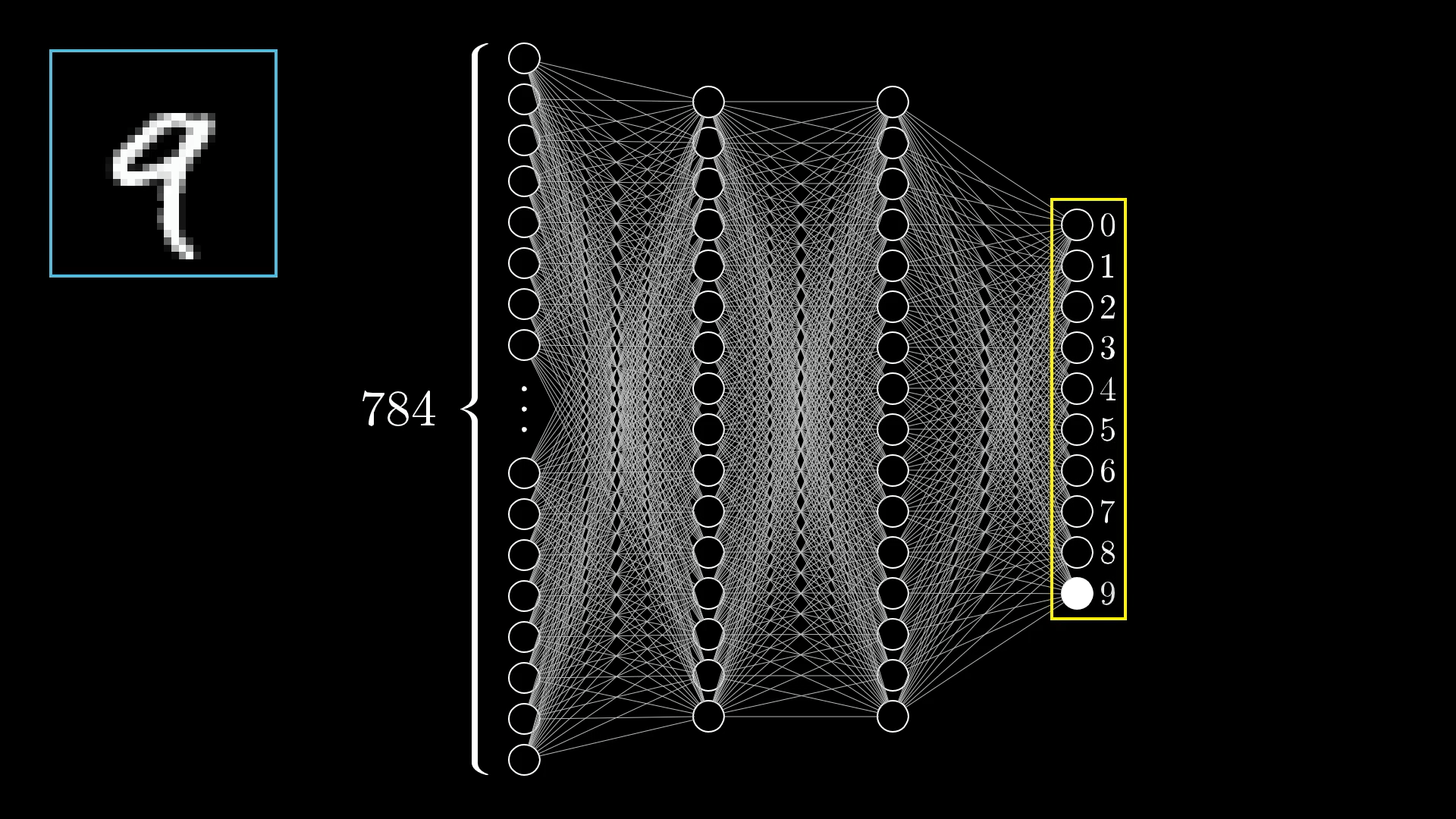
网络的最后一层包含10个神经元，每个神经元代表一个可能的数字结果

神经元的激活同样是0.0到1.0之间的某个数字，这代表着系统认为图像和给定数字的符合程度

隐藏层(The Hidden Layers)

在神经网络的中间会有一些层，这些层被称为”隐藏层”

隐藏层的主要作用就是：进一步处理我们的图像输入

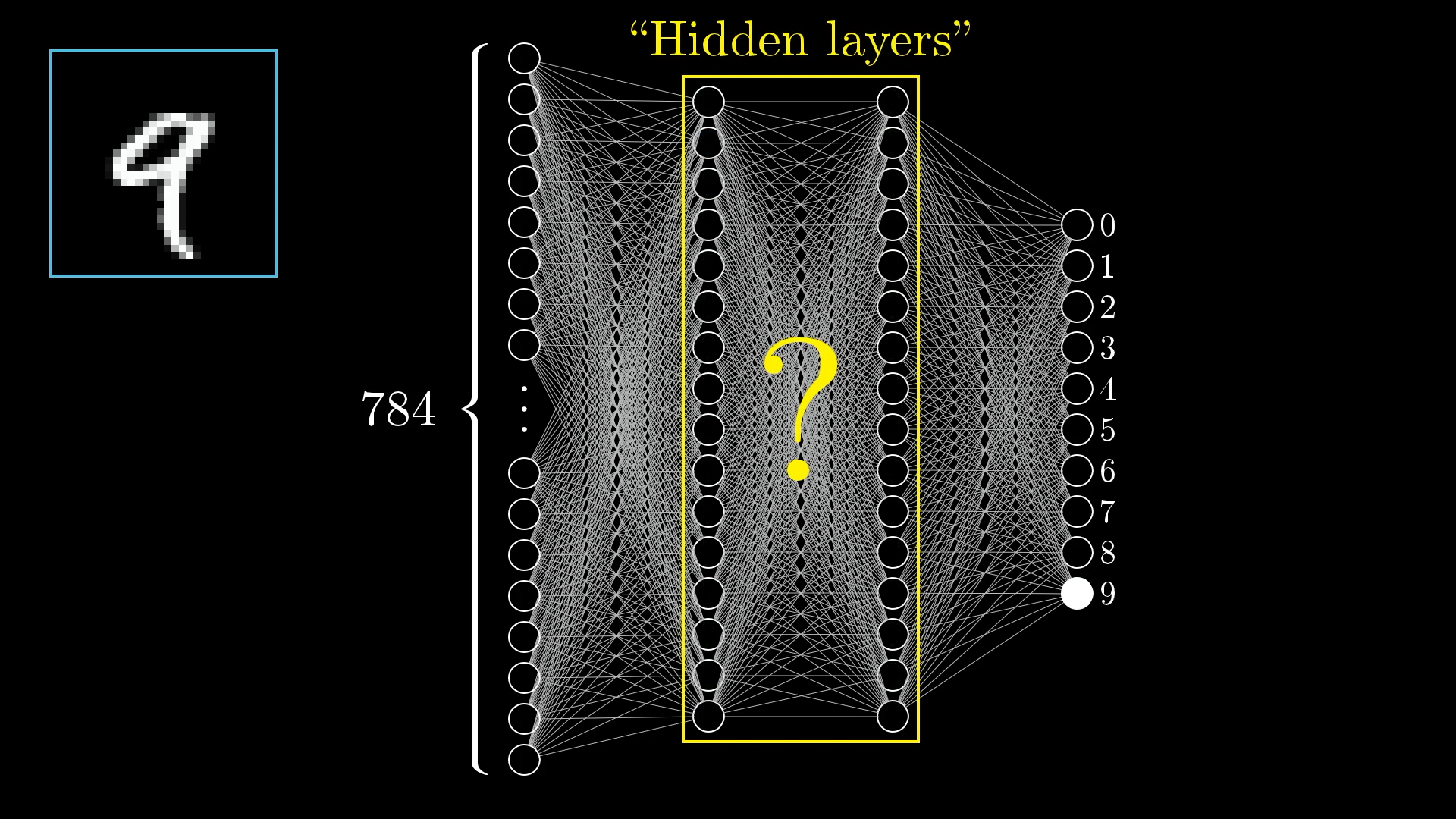
在这些层中，每一层都会对下一层中的每个神经元的激活产生一定影响

当我们人类识别数字的时候，我们可能会数字的线条形状来进行识别，换言之，每个数字都能够被拆分为更小的、能够被识别的子组件

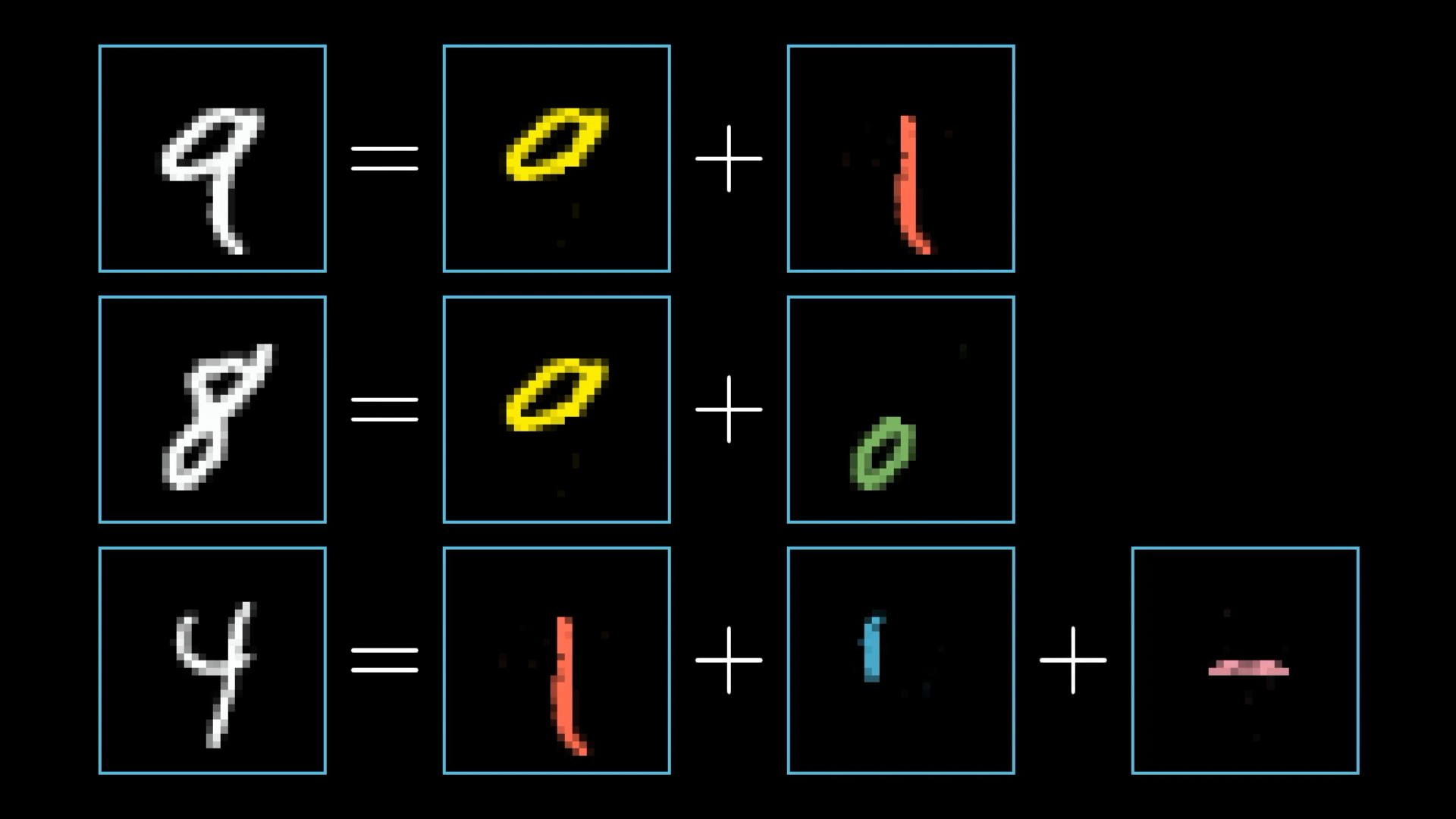
每一层的神经元都在做类似的事情：即尝试识别出这些子组件。最终我们将得到一个近似某个数字的结论

这么说有点不够具象，建议观看原文博客，有生动的影像

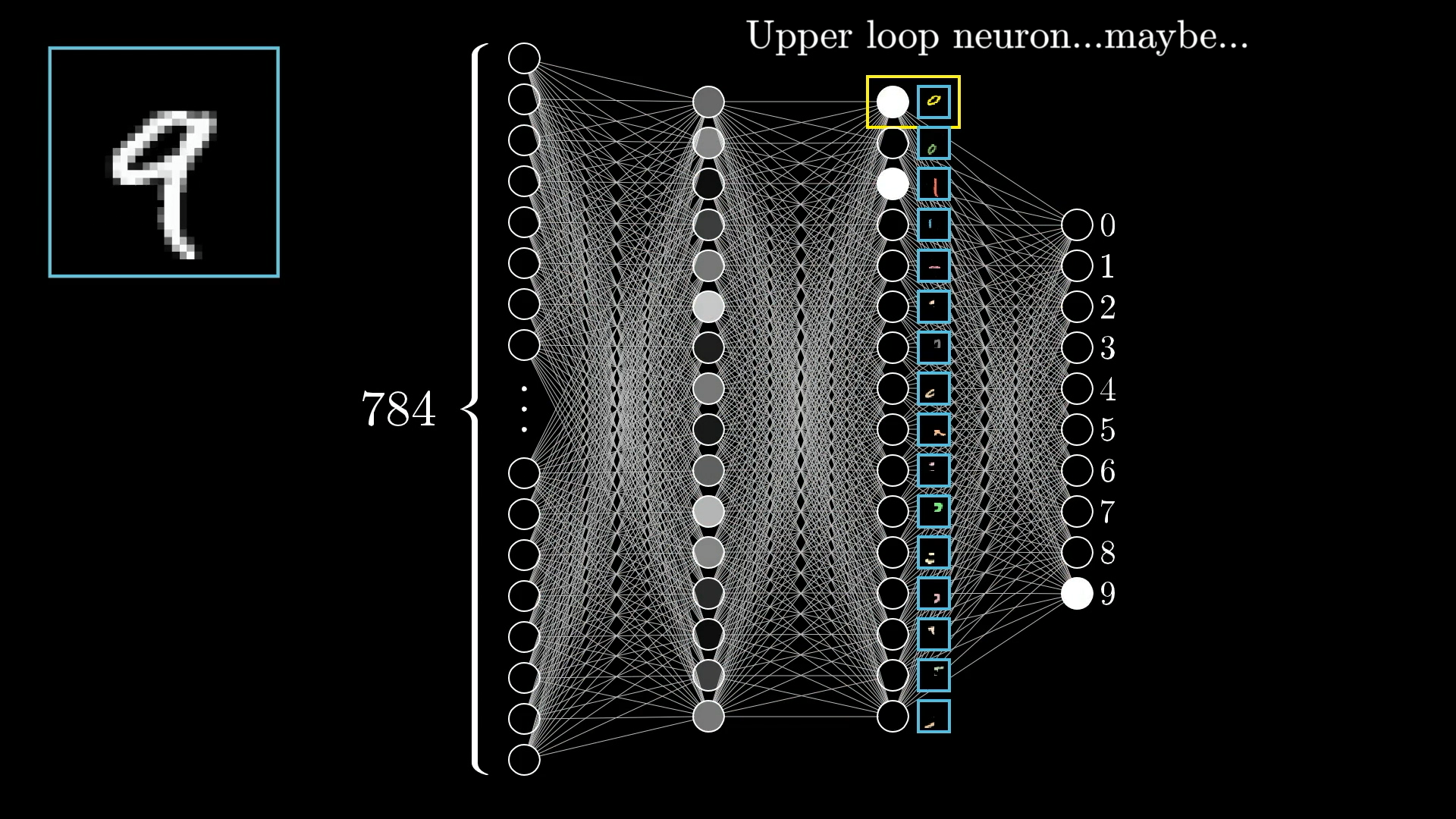
层之间的信息传递

现在我们引入了层的概念，即负责处理神经元输入的一种系统

我们知道，识别数字这个工作是一层一层进行下来的，前文已说过

那么层与层之间是怎么进行信息传递的呢？

这就涉及到一个权重问题

原文我开的翻译说的比较难懂，我尝试使用自己的话解释一遍，可能也不太准确

如下图，我们希望系统能够识别出这个特定区域的线条

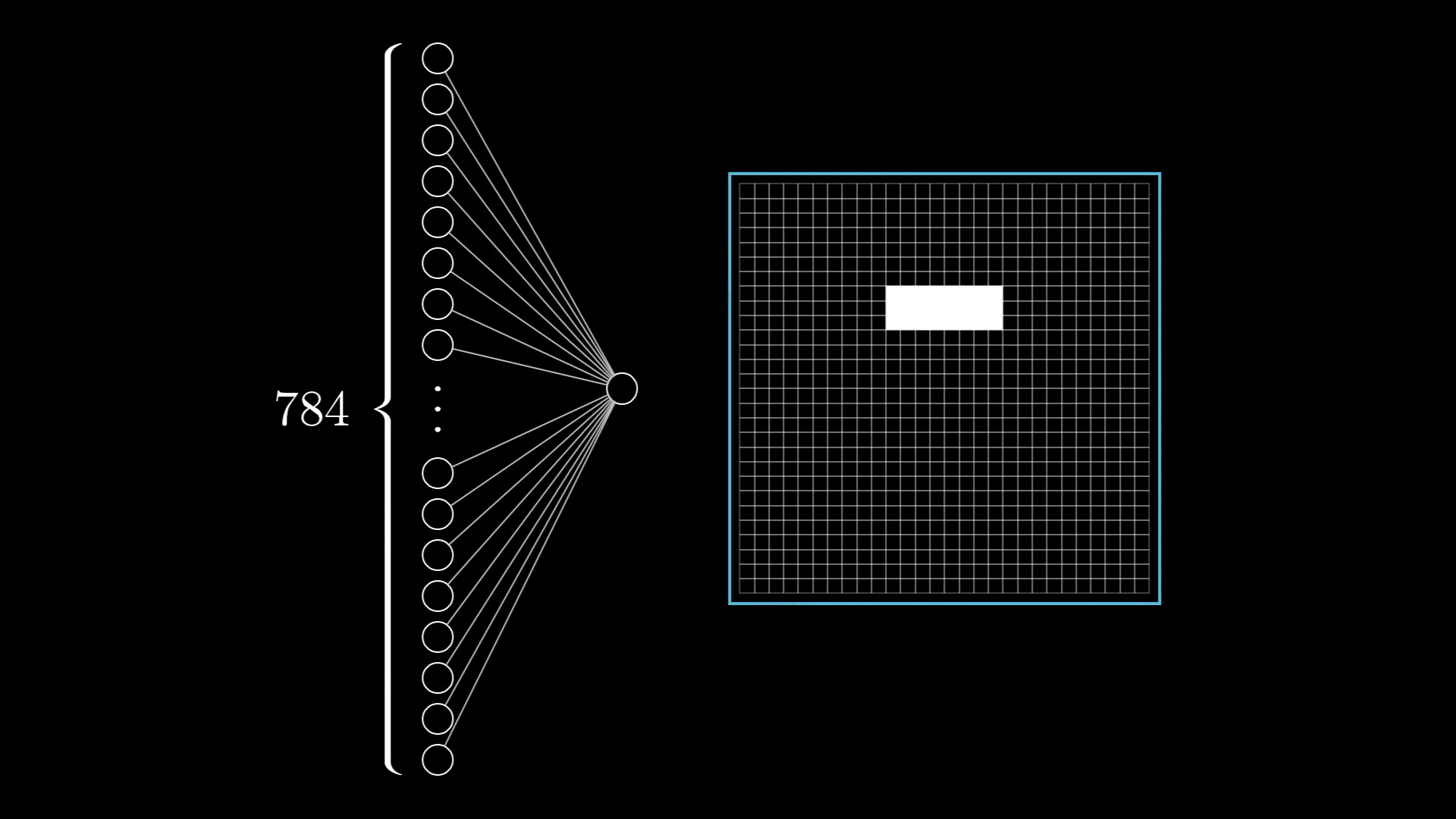
那么，对应这个位置的神经元我们就可以设置得更为“活跃”一些，也就是分配更大的权重。我们识别过程实质上就是每一层的权重叠加，那么特定区域的权重越大，对于我们识别过程的影响也就越大，从而使得我们更容易识别到目标区域

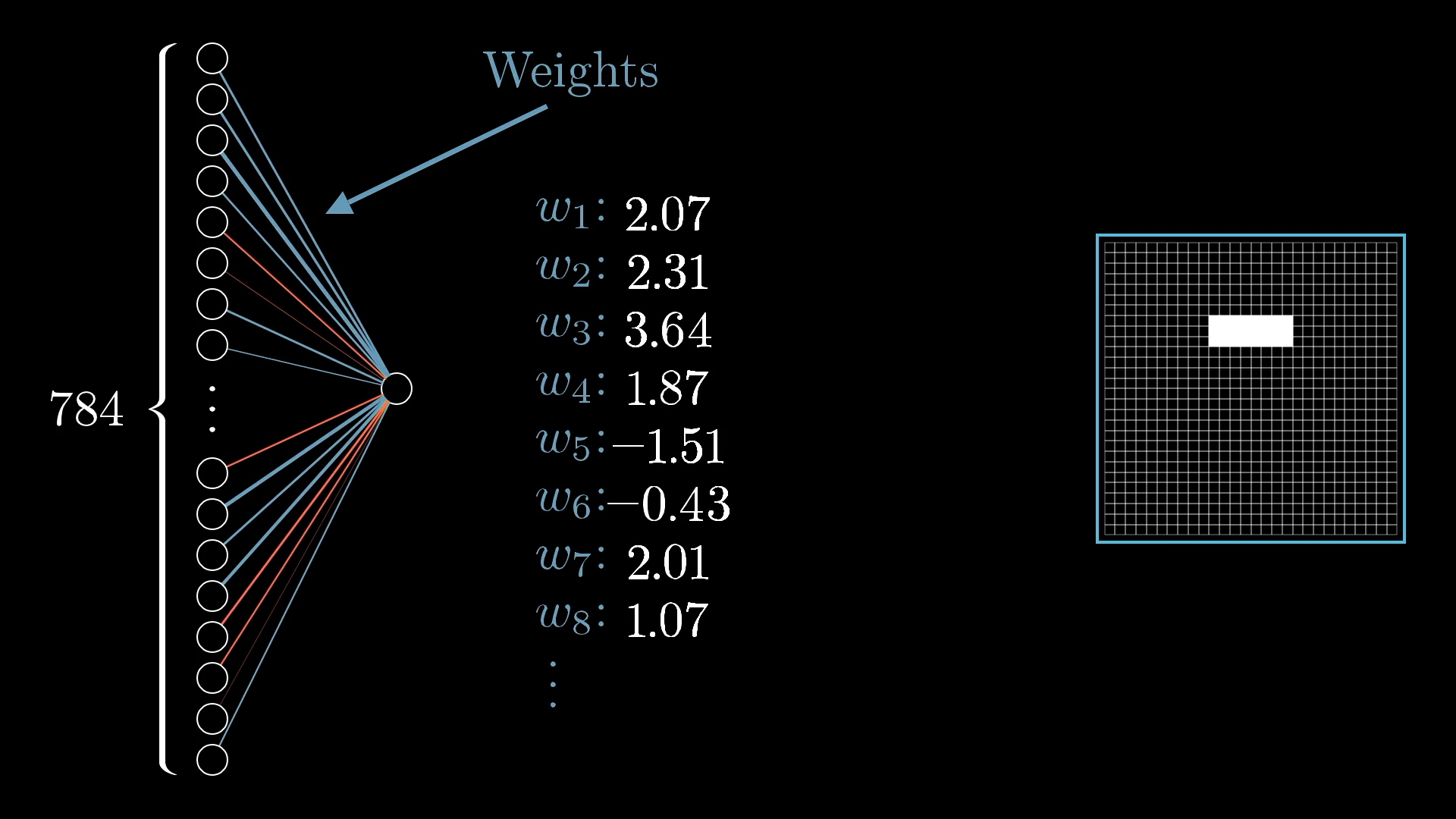
与之对应的，其他非特定区域的神经元对我们识别这个区域的影响较小，我们就可以将其设置为负数。正权重则表示下一层对应的神经元应该打开，负权重则表示应该关闭

因此，当我们实际计算第二层神经元的值时，我们需要从上一层神经元中获取所有的激活值，并计算它们的加权总和

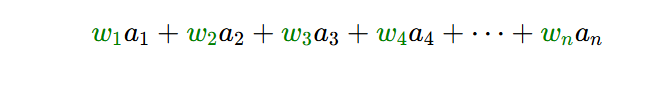
对应权重分散到网格中如图所示

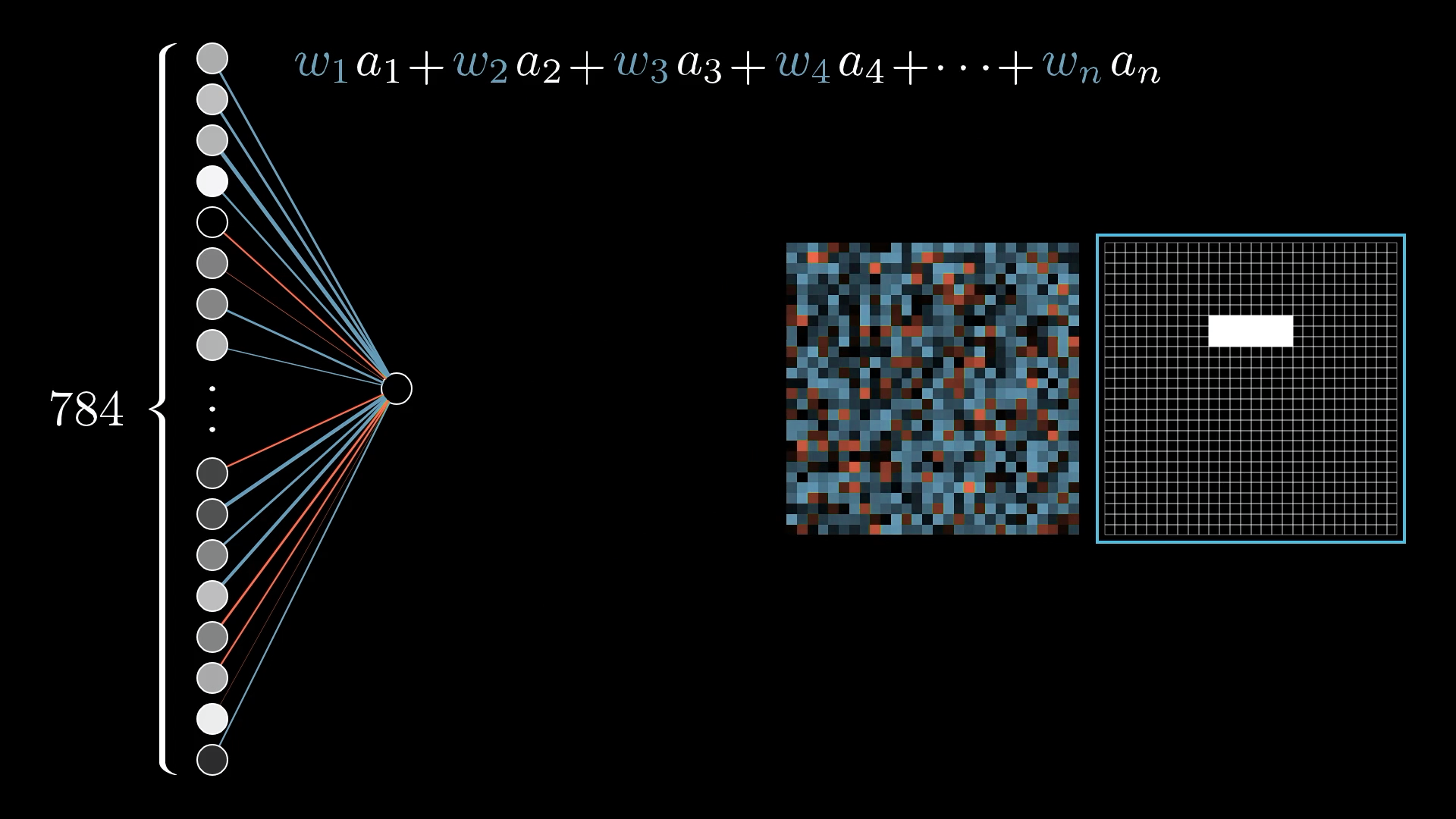
蓝色代表正权重，红色代表负权重

神经网络激活函数（Sigmoid Squishification）

加权和的结果可以是任何数字，但是，对于识别的过程来说，如果加权和的数值太大了，就不利于我们后续的处理

因此我们引入被称为”sigmoid”的函数，也称为逻辑曲线

我们利用这个函数将激活值的加权和压缩至0到1的范围内，从而方便我们后续的处理

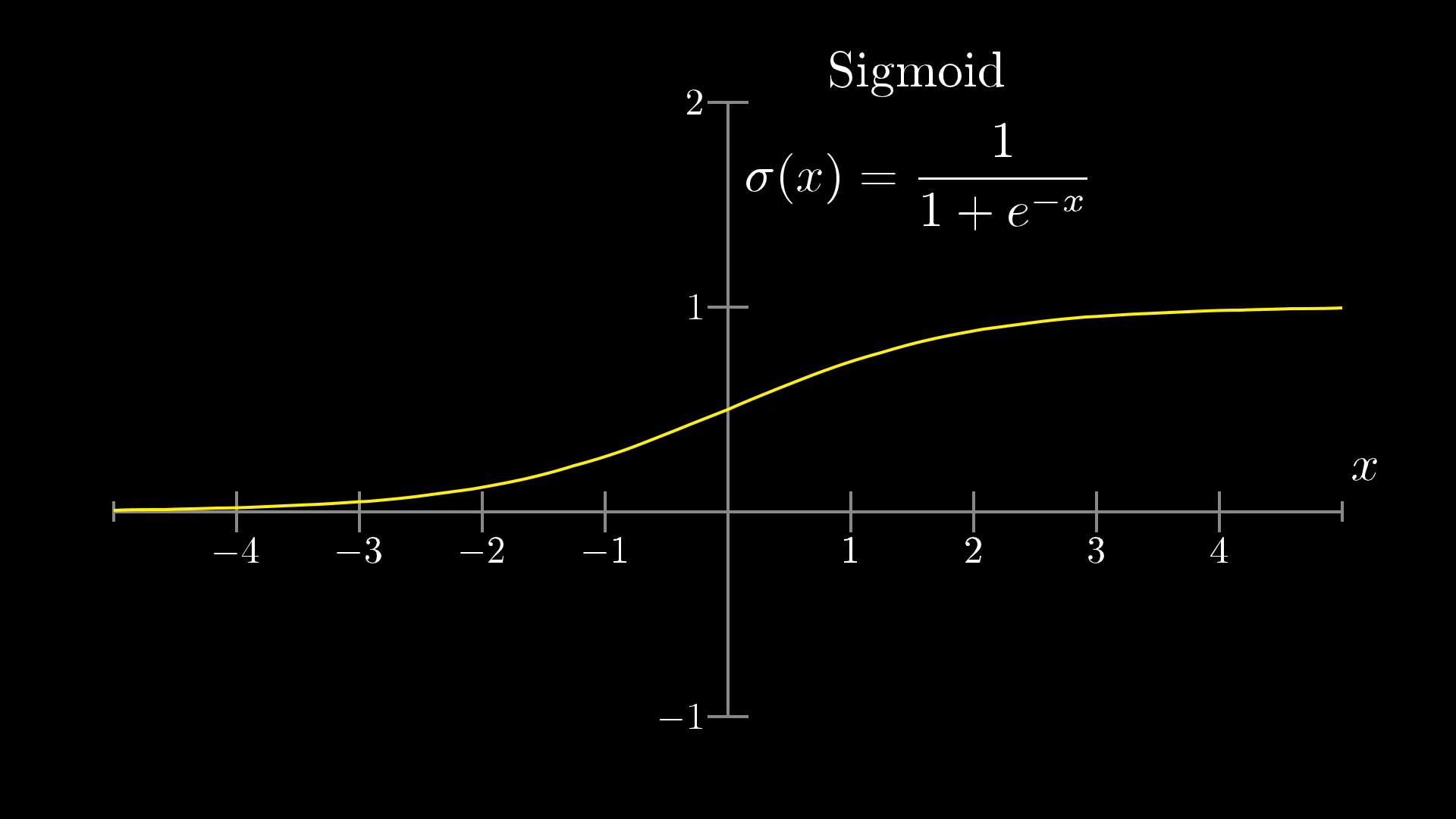
“sigmoid”函数处理负输入时，越小的负输入就越接近0，越大的正数就越接近1，这样使得加权和的值能稳定在一个区间内

当然，不是说神经元的加权和大于0就一定亮起，有的时候我们希望它只在总和大于10时才变为有意义的活跃

而我们所需要做的就是将一些数字（例如-10）添加到加权总和中，然后带入sigmoid函数，将其压缩到0到1的范围内

这个被添加进来的数字，被我们称为**bias，**也就是偏差

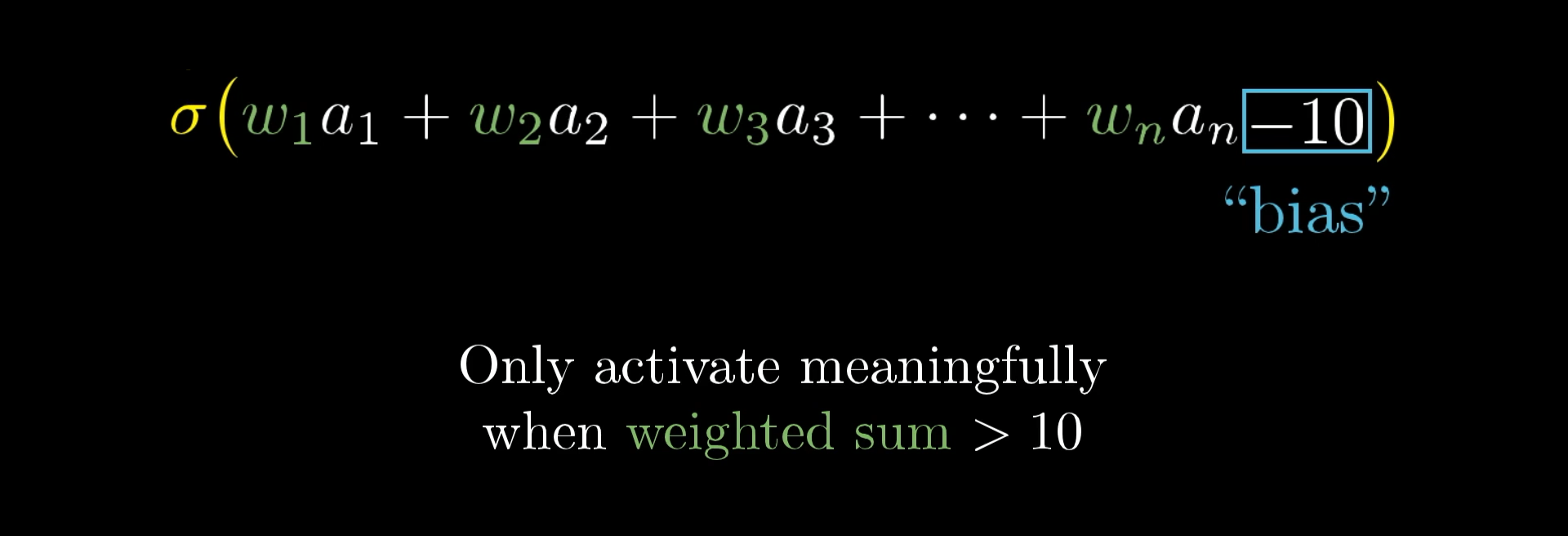
所以我们可以得到一个结论：权重会告诉你第二层的这个神经元在识别什么样的像素模式，而偏差则决定了这个加权和需要达到多大，神经元才能真正被激活起来

后续就是一些线性代数的问题了，不作赘述，感兴趣可以看原文